Pengukuran
penyimpangan adalah suatu ukuran yang menunjukkan tinggi rendahnya
perbedaan data yang diperoleh dari rata-ratanya. Ukuran penyimpangan
digunakan untuk mengetahui luas penyimpangan data atau homogenitas data.
Dua variabel data yang memiliki mean sama belum tentu memiliki
kualitas yang sama, tergantung dari besar atau kecil ukuran
penyebaran datanya. Ada bebarapa macam ukuran penyebaran data, namun
yang umum digunakan adalah standar deviasi.
Macam-macam
ukuran penyimpangan data adalah :
Jangkauan
(range)
Simpangan
rata-rata (mean deviation)
Simpangan
baku (standard deviation)
Varians
(variance)
Koefisien
variasi (Coefficient of variation)
1.
Jangkauan (range)
Range
adalah salah satu ukuran statistik yang menunjukan jarak penyebaran data antara
nilai terendah (Xmin) dengan nilai tertinggi (Xmax). Ukuran ini sudah
digunakan pada pembahasan daftar distribusi frekuensi. Adapun rumusnya adalah
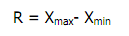
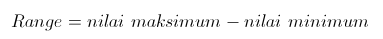
Contoh :
Berikut ini nilai ujian semester dari 3 mahasiswa
A = 60 55 70 65 50 80 40
B = 50 55 60 65 70 65 55
C = 60 60 60 60 60 60 60
Dari data diatas dapat diketahui bahwa
A = memiliki Xmax=80, Xmin= 40 , R = 40 , meanya 60
B = memiliki Xmax=70, Xmin= 50 , R = 20 , meanya 60
C = memiliki Xmax=60, Xmin= 60 , R = 0 , meanya 60
Dari contoh di atas dapat disimpulkan bahwa :
a. Semakin kecil rangenya maka semakin homogen distribusinya
b. Semakin besar rangenya maka semakin heterogen distribusinya
c. Semakin kecil rangenya, maka meannya merupakan wakil yang representatif
d. Semakin besar rangenya maka meannya semakin kurang representatif
2. Simpangan Rata-rata (mean deviation)
Berikut ini nilai ujian semester dari 3 mahasiswa
A = 60 55 70 65 50 80 40
B = 50 55 60 65 70 65 55
C = 60 60 60 60 60 60 60
Dari data diatas dapat diketahui bahwa
A = memiliki Xmax=80, Xmin= 40 , R = 40 , meanya 60
B = memiliki Xmax=70, Xmin= 50 , R = 20 , meanya 60
C = memiliki Xmax=60, Xmin= 60 , R = 0 , meanya 60
Dari contoh di atas dapat disimpulkan bahwa :
a. Semakin kecil rangenya maka semakin homogen distribusinya
b. Semakin besar rangenya maka semakin heterogen distribusinya
c. Semakin kecil rangenya, maka meannya merupakan wakil yang representatif
d. Semakin besar rangenya maka meannya semakin kurang representatif
2. Simpangan Rata-rata (mean deviation)
Simpangan
rata-rata merupakan penyimpangan nilai-nilai individu dari nilai rata-ratanya.
Rata-rata bisa berupa mean atau median. Untuk data mentah simpangan rata-rata
dari median cukup kecil sehingga simpangan ini dianggap paling sesuai untuk
data mentah. Namun pada umumnya, simpangan rata-rata yang dihitung dari mean
yang sering digunakan untuk nilai simpangan rata-rata.
Data
tunggal dengan seluruh skornya berfrekuensi satu
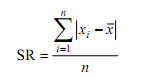
dimana xi merupakan
nilai data
Data
tunggal sebagian atau seluluh skornya berfrekuensi lebih dari satu
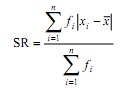
dimana xi merupakan
nilai data
Data
kelompok ( dalam distribusi frekuensi)
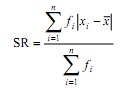
dimana xi merupakan
tanda kelas dari interval ke-i dan fi merupakan frekuensi
interval ke-i
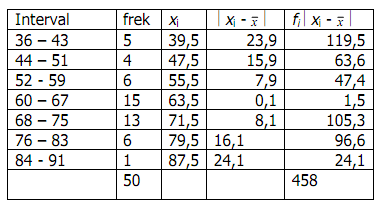
Contoh :
Dari tabel diperoleh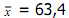
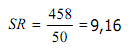
3. Simpangan Baku (standard deviation)
Dari tabel diperoleh
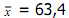

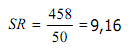
3. Simpangan Baku (standard deviation)
Standar
deviasi merupakan ukuran penyebaran yang paling banyak digunakan. Semua gugus
data dipertimbangkan sehingga lebih stabil dibandingkan dengan ukuran lainnya.
Namun, apabila dalam gugus data tersebut terdapat nilai ekstrem, standar
deviasi menjadi tidak sensitif lagi, sama halnya seperti mean.
Standar
Deviasi memiliki beberapa karakteristik khusus lainnya. SD tidak berubah
apabila setiap unsur pada gugus datanya di tambahkan atau dikurangkan dengan
nilai konstan tertentu. SD berubah apabila setiap unsur pada gugus datanya
dikali/dibagi dengan nilai konstan tertentu. Bila dikalikan dengan nilai
konstan, standar deviasi yang dihasilkan akan setara dengan hasilkali dari
nilai standar deviasi aktual dengan konstan.
Rumus
Simpangan Baku untuk Data Tunggal
untuk
data sample menggunakan rumus
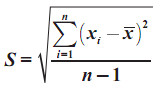
untuk
data populasi menggunkan rumus

Contoh :
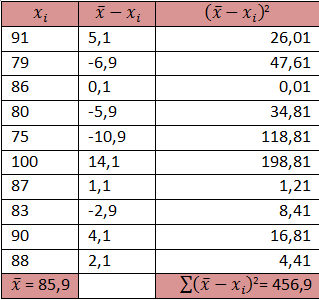
Selama 10 kali ulangan semester ini sobat mendapat nilai 91, 79, 86, 80, 75, 100, 87, 93, 90,dan 88. Berapa simpangan baku dari nilai ulangan sobat?
Selama 10 kali ulangan semester ini sobat mendapat nilai 91, 79, 86, 80, 75, 100, 87, 93, 90,dan 88. Berapa simpangan baku dari nilai ulangan sobat?
Jawab
Soal di atas menanyakan simpangan baku dari data populasi jadi menggunakan rumus simpangan baku untuk populasi.
Kita cari dulu rata-ratanya
rata-rata = (91+79+86+80+75+100+87+93+90+88)/10 = 869/10 = 85,9
Kita masukkan ke rumus
Soal di atas menanyakan simpangan baku dari data populasi jadi menggunakan rumus simpangan baku untuk populasi.
Kita cari dulu rata-ratanya
rata-rata = (91+79+86+80+75+100+87+93+90+88)/10 = 869/10 = 85,9
Kita masukkan ke rumus
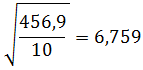
Rumus
Simpangan Baku Untuk Data Kelompok
untuk
sample menggunakan rumus
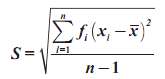
untuk
populasi menggunakan rumus

Contoh
:
Diketahui data tinggi badan 50 siswa samapta kelas c adalah sebagai berikut
Diketahui data tinggi badan 50 siswa samapta kelas c adalah sebagai berikut
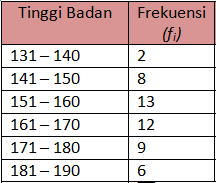
hitunglah
berapa simpangan bakunya

1. Kita cari dulu rata-rata data kelompok tersebut
2. Setelah ketemu rata-rata dari data kelompok tersebut kita bikin tabel untuk memasukkannya ke rumus simpangan baku
4. Varians (variance)
Varians
adalah salah satu ukuran dispersi atau ukuran variasi. Varians dapat
menggambarkan bagaimana berpencarnya suatu data kuantitatif. Varians
diberi simbol σ2 (baca: sigma kuadrat) untuk populasi dan untuk s2 sampel.
Selanjutnya
kita akan menggunakan simbol s2 untuk varians karena umumnya kita hampir
selalu berkutat dengan sampel dan jarang sekali berkecimpung dengan populasi.
Rumus
varian atau ragam data tunggal untuk populasi

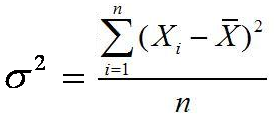
Rumus
varian atau ragam data tunggal untuk sampel
Rumus
varian atau ragam data kelompok untuk populasi
Rumus varian atau ragam data kelompok untuk sampel
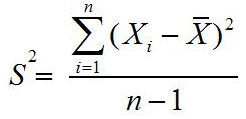
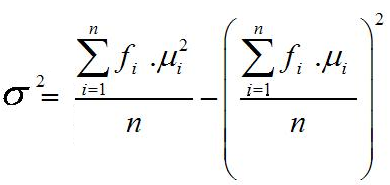
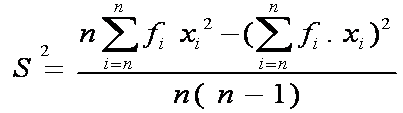
Keterangan:
σ2 = varians atau ragam untuk populasi
S2 = varians atau ragam untuk sampel
fi = Frekuensi
xi = Titik tengah
x¯ = Rata-rata (mean) sampel dan μ = rata-rata populasi
n = Jumlah data
σ2 = varians atau ragam untuk populasi
S2 = varians atau ragam untuk sampel
fi = Frekuensi
xi = Titik tengah
x¯ = Rata-rata (mean) sampel dan μ = rata-rata populasi
n = Jumlah data
5.
Koefisien variasi (Coefficient of variation)
Koefisien
variasi merupakan suatu ukuran variansi yang dapat digunakan untuk
membandingkan suatu distribusi data yang mempunyai satuan yang berbeda. Kalau
kita membandingkan berbagai variansi atau dua variabel yang mempunyai satuan
yang berbeda maka tidak dapat dilakukan dengan menghitung ukuran penyebaran
yang sifatnya absolut.
Koefisien
variasi adalah suatu perbandingan antara simpangan baku dengan nilai rata-rata
dan dinyatakan dengan persentase.


Besarnya
koefisien variasi akan berpengaruh terhadap kualitas sebaran data. Jadi
jika koefisien variasi semakin kecil maka datanya semakin homogen dan jika
koefisien korelasi semakin besar maka datanya semakin heterogen.
Diposkan
oleh
Tidak ada komentar:
Posting Komentar